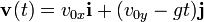TIRO PARABÓLICO
El tiro parabólico es un ejemplo de movimiento realizado por un cuerpo en dos dimensiones o sobre un plano. Algunos ejemplos de cuerpos cuya trayectoria corresponde a un tiro parabólico son: proyectiles lanzados desde la superficie de la Tierra o desde un avión, el de una pelota de fútbol al ser despejada por el portero, el de una pelota de golf al ser lanzada con cierto ángulo respecto al eje horizontal.
El tiro parabólico es la resultante de la suma vectorial del movimiento horizontal uniforme y de un movimiento vertical rectilíneo uniformemente variado. El tiro o movimiento parabólico es de dos clases:
TIRO PARABÓLICO HORIZONTAL
Se caracteriza por la trayectoria o camino curvo que sigue un cuerpo al ser lanzado al vacío, resultado de dos movimientos independientes: un movimiento horizontal con velocidad constante y otro vertical, el cual se inicia con una velocidad cero y va aumentando en la misma proporción de otro cuerpo que se dejara caer del mismo punto en el mismo instante. La forma de la curva descrita es abierta, simétrica respecto a un eje y con solo foco, es decir, es una parábola. Por ejemplo en la figura 1 sé gráfica el descenso al mismo tiempo de dos pelotas, solo que la pelota del lado derecho es lanzada con una velocidad horizontal de 15 m/s. Al término del primer segundo ambas pelotas han recorrido 4.9 m en su caída, sin embargo, la pelota de la derecha también ha avanzado 15 m respecto a su posición inicial. A los dos segundos ambas pelotas ya han recorrido 19.6 m en su caída, pero la pelota de la derecha ya lleva 30 m recorridos de su movimiento horizontal. Si se desea calcular la distancia recorrida en forma horizontal puede hacerse con la expresión: d = vt, pues la pelota lanzada con una velocidad horizontal tendrá una rapidez constante durante su recorrido horizontal e independiente de su movimiento vertical originado por la aceleración de la gravedad durante su caída libre.
La trayectoria descrita por un proyectil cuya caída es desde un avión en movimiento, es otro ejemplo de tiro parabólico horizontal. Supongamos que un avión vuela a 250 m/s y deja caer un proyectil, la velocidad adquirida por dicho proyectil en los diferentes momentos de su caída libre, se puede determinar por medio del método del paralelogramo; para ello, basta representar mediante vectores las componentes horizontal y vertical del movimiento. Al primer segundo de su caída la componente tendrá un valor de 9.8 m/s, mientras la componente horizontal de su velocidad será la misma que llevaba el avión al soltar el proyectil, es decir, 250 m/s. Trazamos el paralelogramo y obtenemos la resultante de las dos velocidades. Al instante dos segundo la componente vertical tiene un valor de 19.6 m/s y la horizontal, como ya señalamos, conserva su mismo valor: 250 m/s. Así continuaríamos hasta que el proyectil llegue al suelo. En la figura 2 vemos cuáles serían las componentes rectangulares de la velocidad de un cuerpo, el cual sigue una trayectoria parabólica horizontal.
Componentes rectangulares de la velocidad resultante (VR) de un cuerpo que sigue una trayectoria parabólica horizontal. Se observa como la velocidad horizontal (VH) permanece constante, mientras la velocidad vertical (VV) aumenta durante su caída libre por acción de la gravedad de la Tierra.
Tiro Horizontal
Tiro horizontal
Movimiento de media parábola:
El movimiento de media parábola o semiparabólico (lanzamiento horizontal)
se puede considerar como la composición de un avance horizontal rectilíneo uniforme y la caída libre.
El movimiento parabólico completo:
Se puede considerar como la composición de un avance horizontal rectilíneo uniforme y un lanzamiento vertical hacia arriba, que es un movimiento rectilíneo uniformemente acelerado hacia abajo (MRUA) por la acción de la gravedad.
En condiciones ideales de resistencia al avance nulo y campo gravitatorio uniforme, lo anterior implica que:
Un cuerpo que se deja caer libremente y otro que es lanzado horizontalmente desde la misma altura tardan lo mismo en llegar al suelo.
La independencia de la masa en la caída libre y el lanzamiento vertical es igual de válida en los movimientos parabólicos.
Un cuerpo lanzado verticalmente hacia arriba y otro parabólicamente completo que alcance la misma altura tarda lo mismo en caer.
TIRO HORIZONTAL
El movimiento que realiza un móvil que es una rama de parábola, se llama tiro horizontal. Si la velocidad de salida es v0, tendremos que las componentes de la velocidad inicial son: v0x=v0 v0y = 0
Como ocurría en el caso del tiro parabólico, este movimiento puede considerarse el resultado de componer dos movimientos simultáneos e independientes entre sí: uno, horizontal y uniforme; otro, vertical y uniformemente acelerado. Las propiedades cinemáticas del cuerpo en cualquier instante (t) de su movimiento son:
Magnitud Componente x Componente y
Aceleración ax = 0 ay = -g
velocidadvx = v0 vy = - gt
posición x = v0t y = h -(1/2)gt
2
Lo que nos queda es demostrar como aplicaremos la teoría anteriormente observada a nuestro proyecto áulico realizado con materiales caseros. Para ello haremos de cuenta que nuestro experimento es un cañón manual y plantearemos un problema para dicho elemento. Un cañón lanza un proyectil formando un ángulo de 60º con la horizontal. Demostrar que si logramos hallar el tiempo que tarda el proyectil en su trayectoria desde que sale del dispositivo
hasta que llega al suelo (o al nivel donde estaba situado el dispositivo), podremos obtener la altura máxima (H) y la distancia (horizontal) la cual se desplaza nuestro proyectil.
Lo primero que haremos es tomar el tiempo desde que el proyectil sale del dispositivo hasta
que toca tierra. Una vez hecho esto y teniendo en cuenta que cuanto el cuerpo llega a la altura
máxima, la velocidad vertical es nula:
v¨=v¨°- g×t=0 de aquí t= v¨°/ g
Una vez hecho esto ya conocemos la velocidad vertical inicial entonces reemplazamos este valor en la fórmula de H, y obtenemos: H= v¨° × (v¨°/g) - ½ g × (v¨°/g)² = (v¨°²/g) - ½ ( v¨°²/g)= ½
(v¨°²/g). De aquí obtenemos:
H= (v¨°)² /2g » el resultado es la altura máxima que alcanza el proyectil.
Llamamos alcance a la distancia horizontal recorrida por el proyectil desde que sale del cañón hasta que toca el suelo. Como el movimiento horizontal es uniforme, si llamamos d al
alcance, será: d= v° × t
Para obtener v° aplicamos la fórmula: v°= v¨°/ sen a. Para poder calcular d es necesario conocer t, tiempo que tarda el proyectil en llegar al suelo.
Pero la parábola es una figura geométrica, de modo que si el proyectil tarda (v°.sen á/g) en alcanzar su altura máxima, tardará otro tanto en volver al suelo. De modo que:
v°= v´° / cos a d= v´° × 2t= v° × cos a ×[( 2v° × sen a)/g]= (2 v°² × sen a × cos a)/ g . t=tiempo d=distancia v°=velocidad inicial v´°=velocidad inicial horizontal v¨°=velocidad inicial vertical
g= aceleración de la gravedad.
Cabe aclarar que durante el transcurso de este trabajo, la experiencia relatada anteriormente,
así como la teoría antes presentada fue parte de un trabajo diario durante las clases de física. Con éxito hemos confirmado nuestra hipótesis acerca de la fluidez y la dinámica que se llevó a cabo en dichas clases. El interés no solo por parte de alumnos, sino la sencillez y practicidad para el desarrollo de estos temas por parte del docente nos lleva a la grata confirmación que la propuesta de trabajo se refiere a componentes formales y básicos presentes en todo proceso de innovación educativa.
En definitiva, este trabajo pretende orientar las posibles iniciativas de innovación educativa que los docentes se propongan iniciar en sus respectivas aulas. La propuesta se ofrece como un esquema formal de tareas que pueden aplicarse a contenidos de innovación muy diversos
desde las formas de evaluar en el aula hasta los modos de participación de los estudiantes. Es
recomendable que las propuestas de cambio que elijamos se encuentren dentro de las posibilidades de cada uno, no importa que parezcan tan pequeñas como un granito de arena, lo importante es aprender a comprometerse a innovar, y comprobar que toda transformación por pequeña que parezca, si es auténtica, implica modificaciones en todos los aspectos.
Referencias Bibliográficas:
Tiro Parabólico
Es resultado de la combinación de dos movimientos independientes; el primero es un movimiento uniformemente acelerado (MRUA), que se expresa en forma de tiro vertical durante el ascenso y como caída libre desde el momento en que empieza a descender. El segundo es un movimiento horizontal rectilíneo uniforme (MRU), cuya característica es que la velocidad permanece constante todo el recorrido. El tiro parabólico es un movimiento que se efectúa en dos dimensiones o sobre un plano.
Los puntos de mayor interés para describir este movimiento son:
Angulo de disparo: Es la inclinación con la que sale impulsado el proyectil. Se mide respecto al plano horizontal.
Velocidad inicial: Es la velocidad con que el proyectil emprende el movimiento de tiro parabólico y que es suministrado por un agente externo.
Altura máxima: Mayor altura que alcanza el objeto, medida desde el plano horizontal desde donde fue efectuado el disparo. En este punto la componente vertical de la velocidad es cero y solo se presenta componente horizontal.
Alcance: Es la distancia que recorre el proyectil, medida en sentido horizontal desde el punto inicial de disparo hasta el punto de caída, que se encuentra al mismo nivel que el primero.
Alcance máximo: Es la mayo distancia horizontal que recorre el proyectil. Se consigue exclusivamente para un Angulo de 45°.
Es impórtate conocer que dirección se considera positiva, una vez elegida la dirección positiva.
El desplazamiento será: positivo (+) si esta por encima del punto de partida y negativo (-) si esta por debajo del punto de partida.
La velocidad será: positiva (+) su el movimiento es a favor de la dirección elegida como positiva y negativa (-) si el movimiento es en contra de la dirección elegida como positiva.
La aceleración será: Positiva (+) si la fuerza esta a favor de la dirección elegida como positiva y negativa (-) su ka fuerza esta en contra de la dirección elegida como positiva.
La dirección positiva es hacia abajo para la caída libre y hacia arriba para el tiro vertical. Ambos son movimientos rectilíneos uniformemente acelerados, debido a que la aceleración de la gravedad es constante (g=9,81 m/s2).
Sea un proyectil lanzado desde un cañón. Si elegimos un sistema de referencia de modo que la dirección Y sea vertical y positiva hacia arriba, a y = - g y a x = 0. Además suponga que el instante t = 0, el proyectil deja de origen (X i = Y i = 0) con una velocidad Vi.
Si vi. Hace un ángulo Qi con la horizontal, a partir de las definiciones de las funciones sen y cos se obtiene:


Como el movimiento de proyectiles es bi-dimencional, donde ax = 0 y ay = -g, o sea con aceleración constante, obtenemos las componentes de la velocidad y las coordenadas del proyectil en cualquier instante t, con ayuda de las ecuaciones ya utilizadas para el M.R.U.A. Expresando estas en función de las proyecciones tenemos:
Si un proyectil es lanzado horizontalmente desde cierta altura inicial, el movimiento es semi-parabólico.
Las ecuaciones del movimiento considerando Vyi = 0 serían:
Combinando las ecuaciones arriba explicadas para el movimiento parabólico podemos algunas obtener ecuaciones útiles:
- Altura máxima que alcanza un proyectil:
- Tiempo de vuelo del proyectil:
- Alcance del proyectil :
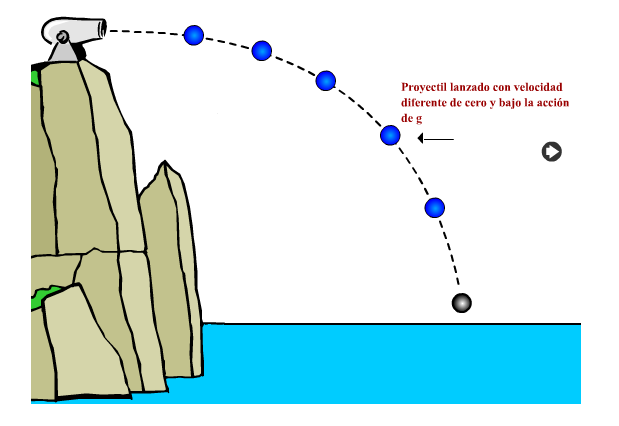
Hay dos ecuaciones que rigen el movimiento parabólico:
Es el módulo de la velocidad inicial.
 Es el ángulo de la velocidad inicial sobre la horizontal.
Es el ángulo de la velocidad inicial sobre la horizontal. Es la aceleración de la gravedad.
Es la aceleración de la gravedad.
la velocidad inicial se compone de dos partes:
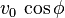
que se denomina componente horizontal de la velocidad inicial. En lo sucesivo
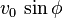 que se denomina componente vertical de la velocidad inicial. En lo sucesivo
que se denomina componente vertical de la velocidad inicial. En lo sucesivo
Se puede expresar la velocidad inicial de este modo:
 : [ecu. 1]
: [ecu. 1]
Será la que se utilice, excepto en los casos en los que deba tenerse en cuenta el ángulo de la velocidad inicial
Ecuación de la aceleración:
La única aceleración que interviene en este movimiento es la de la gravedad, que corresponde a la ecuación:

que es vertical y hacia abajo
Ecuación de la velocidad:
La velocidad de un cuerpo que sigue una trayectória parabólica se puede obtener integrando la siguiente ecuación:

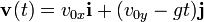

Referencias Bibliográficas:
Mecánica
Mecánica
Es la ciencia que describe y predice condiciones de reposo o movimiento de los cuerpos bajo la acción de fuerzas.
Como todas las demás ciencias que se dividen el trabajo, la Mecánica no es la excepción. Para ser mas precisos, la Mecánica se divide en tres partes:
1. Mecánica de cuerpos rígidos
2. Mecánica de cuerpos deformables
3. Mecánica de fluidos
Mecánica de cuerpos rígidos.
Un cuerpo rígido se puede definir como aquel que no se deforma, se supone que la mayoría de los cuerpos considerados en la mecánica elemental son rígidos. Mas sin embargo, las estructuras y maquinas reales nunca han tenido la posibilidad de considerarse lo absolutamente rígidas ya que se pueden deformar bajo la acción de las cargas que actúan sobre ellas. A pesar de esto, en lo general esas deformaciones son muy pequeñas y no pueden afectar las condiciones de equilibrio o de movimiento de la estructura que se toma en consideración. No obstante, tales deformaciones son importantes en lo que concierne a la resistencia en la falla de las estructuras y se consideran en el estudio de materiales.
Dentro de lo que son los cuerpos rígidos se estudia el efecto de las fuerzas ejercidas sobre un cuerpo rígido y ver como reemplazar un sistema de fuerzas dado por un sistema equivalente más simple. Este análisis se basa en la suposición fundamental de que el efecto de una fuerza dada sobre un cuerpo rígido permanece inalterado si dicha fuerza se mueve a lo largo de su línea de acción. Por tanto, las fuerzas que actúan sobre un cuerpo rígido pueden representarse por vectores deslizante.
Dos conceptos fundamentales de que el efecto de una fuerza sobre un cuerpo rígido son el momento de una fuerza con respecto a un punto y el momento de una fuerza con respecto a un eje. Como la determinación de estas cantidades involucra el calculo de productos escalares y vectoriales de dos vectores. Otro concepto relacionado a esto es el de un par, esto es, la combinación de dos fuerzas que tengan la misma magnitud, líneas de acción paralela y sentidos opuestos. Como se vera, cualquier sistema de fuerzas que actúa sobre un cuerpo rígido puede ser reemplazado por un sistema equivalente que consta de una fuerza, que actúa en cierto punto, y un par. Este sistema básico recibe el nombre de sistema fuerza-par. En el caso de fuerzas concurrentes, coplanares o paralelas, el sistema equivalente fuerzas-par se puede reducir a una sola fuerza, denominada la resultante del sistema, o a un solo par llamado el par resultante del sistema.
Mecánica de cuerpos deformables.
Como se mencionó al comienzo, los cuerpos rígidos no existen; el concepto de cuerpo rígido es puramente ideal ya que todos los cuerpos se deforman cuando están sometidos a fuerzas. Muchas veces estas deformaciones son imperceptibles y para poderlas determinar se requiere de aparatos de medición más o menos sofisticados. Que un material se deforme más o menos, depende de varios factores entre los cuales se pueden citar las cargas a que está sometido, la forma y dimensiones y sus propiedades mecánicas; resistencia, ductilidad, etc.
Mecánica de fluidos.
es la rama de la mecánica de medios continuos (que a su vez es una rama de lafísica) que estudia el movimiento de los fluidos (gases y líquidos) así como lasfuerzas que los provocan.1 La característica fundamental que define a los fluidoses su incapacidad para resistir esfuerzos cortantes (lo que provoca que carezcan de forma definida). También estudia las interacciones entre el fluido y el contorno que lo limita. La hipótesis fundamental en la que se basa toda la mecánica de fluidos es la hipótesis del medio continuo
Proyectil.
Un proyectil es un objeto al cual se ha comunicado una velocidad inicial y se ha dejado en libertad para que realice un movimiento bajo la acción de la gravedad. Los proyectiles que están cerca de la Tierra siguen una trayectoria curva muy simple que se conoce como parábola. Para describir el movimiento es útil separarlo en sus componentes vertical y horizontal.
Por eso es importante explicar el movimiento de un proyectil como resultado de la superposición de un movimiento rectilíneo uniforme y uno uniformemente variado, estableciendo las ecuaciones de la curva representativa, tiempo de vuelo, tiempo máximo, altura máxima, alcance máximo, velocidad y coordenadas de posición en el plano
El término proyectil se aplica por ejemplo a una bala disparada por un arma de fuego, a un cohete después de consumir su combustible, a un objeto lanzado desde un avión o en muchas actividades deportivas (golf, tenis, fútbol, béisbol, atletismo etc.). Los fuegos artificiales y las fuentes del agua son ejemplos del movimiento de proyectiles. El camino seguido por un proyectil se denomina trayectoria. El estudio del movimiento de proyectiles es complejo debido a la influencia de la resistencia del aire, la rotación de la Tierra, variación en la aceleración de la gravedad.










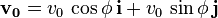



 Es la aceleración de la gravedad.
Es la aceleración de la gravedad.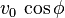

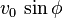
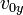
 :
: